

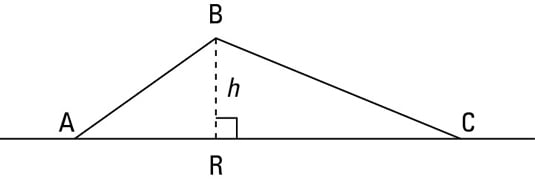
This puts ∠ A to the bottom left, and ∠ B to the bottom right.Ĭonstruct an altitude (or height) h from the interior right angle C to hypotenuse c (so it is perpendicular to c). The right triangle altitude theorem tells us that the altitude of a right triangle drawn to the hypotenuse c forms two similar right triangles that are also similar to the original right triangle.Ĭonstruct △ A B C so that hypotenuse c is horizontal and opposite right angle C, meaning legs a and b are intersecting above c to form the right angle C.
Definition of a altitude geometry how to#
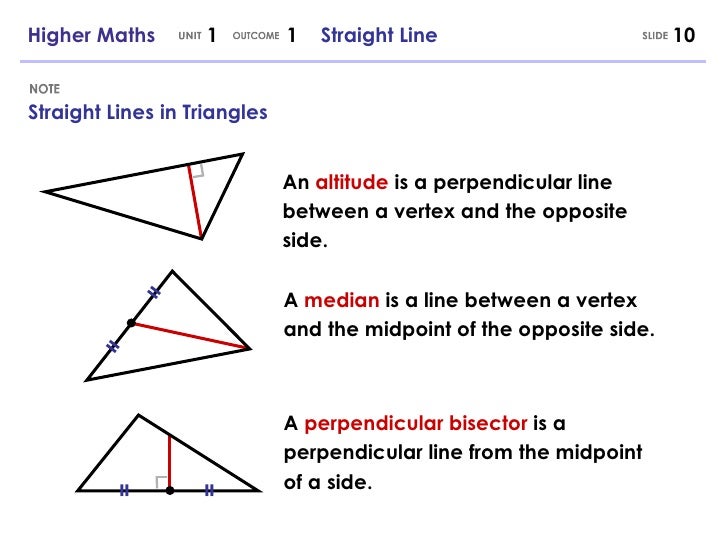
Learn how to use the Pythagorean Theorem to calculate the length of one side of a right triangle. The sides opposite the complementary angles are the triangle's legs and are usually labeled a and b. The other two angles in a right triangle add to 90 ° they are complementary. Opposite it is the triangle's hypotenuse, the longest of the three sides, usually labeled c. We already know the square vertex of the right triangle is a right angle. "Right" refers to the Latin word rectus, meaning "upright." Hypotenuse and Sides of a Right Triangle The term "right" triangle may mislead you to think "left" or "wrong" triangles exist they do not. In drawing right triangles, the interior 90 ° angle is indicated with a little square □ in the vertex. When one of those interior angles measures 90 °, it is a right angle and the triangle is a right triangle. Prove the right triangle altitude theoremĪll triangles have interior angles adding to 180 °.Understand the identifying property of right triangles.After viewing the video, looking over the pictures, and reading the lesson, you will be able to:


 0 kommentar(er)
0 kommentar(er)
